Archiv der Kategorie: descriptive-set-theory

Notiz zur Inklusionsbeziehung in der Borel-Hierarchie

Veröffentlicht am von
Antwort

Sei {(X, \tau)} ein topologischer Raum, jede belieibige Vereinigung offener Mengen liefert eine offene Menge und jeder beliebige Schnitt abgeschlossener Mengen eine abgeschlossene Menge, unter beliebigen Schnitt sind die offenen Mengen und unter beliebiger Vereinigung sind die abgeschlossenen Mengen allerdings nicht abgeschlossen. Diese Beobachtung zusammen mit der Fragestellung welche Mengen man mit Schnittoperationen aus offenen Mengen bzw. mit Vereinigungen aus abgeschlossenen Mengen konstruieren kann führt auf die Borel-Mengen. Im folgenden ist nur die untere Hierarchie interessant, ich definiere daher.

def_mengen

Da eine abzählbare Vereinigung einer abzählbaren Vereinigung von Mengen als abzählbare Vereinigung dieser Mengen geschrieben werden kann (und analoges für Schnitt) muss man abzählbare Vereinigung und abzählbaren Schnitt in obigen Mengen abwechseln um immer wieder neue Mengen konstruieren zu können. Weiterin gilt nach Definition {F = \{ X^C : X \in G \}}. Damit folgt z.B. 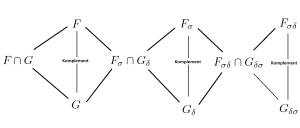für {X \in G_{\delta}} mit {X = \bigcap_{n} O_n} dass {X^C = \bigcup_{n} O_n^C} mit {O_n^C \in F} also {X^C \in F_{\sigma}} und umgekehrt, und {X \in G_{\delta\sigma}} mit {X = \bigcup_n Y_n} mit {Y_n \in G_{\delta}}, also {X^C = \bigcap_n Y_n^C} mit {Y_n^C \in F_{\delta}} und umgekehrt, es liegt das Komplement also jeweils in der “gegenüberliegenden“ {F_{irgendwas}} oder {G_{irgendwas}} Menge.

Wenn man jetzt zur Borel-Hierarchie nachschlägt, so findet man sehr schnell Diagramme, welche die Inklusion {F, G \subseteq F_{\sigma}\cap G_{\delta}} suggerieren, dies gilt aber im Allgemeinen nicht! Betrachte eine überabzählbare Menge {X} und definiere {Y \subseteq X} als offen genau dann wenn {Y^C} endlich ist. Dann gilt {F = \{ Y \subseteq X : Y\mbox{ ist endlich } \}}, {F_{\sigma}} umfasst genau die abzählbaren Mengen, und {G_{\delta}} jene deren Komplement abzählbar ist. Da {X} überabzählbar schließen sich {F_{\sigma}} und {G_{\delta}} aus, d.h. {F_{\sigma} \cap G_{\delta} = \emptyset}.

In metrischen Räumen ist die Welt aber wieder in Ordnung, denn hier gilt

\displaystyle F,G \subseteq F_{\sigma}\cap G_{\delta} \subseteq F_{\sigma}, G_{\delta} \subseteq F_{\sigma\delta}\cap G_{\delta\sigma} \subseteq F_{\sigma\delta}, G_{\delta\sigma}.

Beweis: Sei {(X,d)} metrischer Raum und {C \in F} eine abgeschlossene Menge. Dann gilt

\displaystyle C = \bigcap_{n=1}^{\infty} \bigcup_{x \in C} B\left(x, \frac{1}{n}\right).

Für jedes {n \in \mathbb N} und {x \in C} gilt {\{ x \} \subseteq B(x, 1/n)}, also {C = \bigcup_{x \in C} \{x\} \subseteq \bigcup_{x\in C} B(x, 1/n)}. Da also {C \subseteq \bigcup_{x\in C} B(x, 1/n)} für alle {n} ist {C \subseteq \bigcap_{n=1}^{\infty} \bigcup_{x\in C} B(x, 1/n)}. Sei nun umgekehrt {y \in \bigcap_{n=1}^{\infty} \bigcup_{x \in C} B\left(x, \frac{1}{n}\right)}, d.h. für jedes {n} existiert ein {x_n} mit

\displaystyle y \in B(x_n, 1/n)

oder {d(x_n, y) < 1/n}, d.h. es ist {x_n \rightarrow y} und weil {C} abgeschlossen {y \in C}. Damit folgt erstmal {F \subseteq G_{\delta}}. Durch Übergang zum Komplement folgt {G \subseteq F_{\sigma}}, die Inklusionen {G \subseteq G_{\delta}} und {F \subseteq F_{\sigma}} sind trivial, es folgt also der erste Teil {F,G \subseteq F_{\sigma}\cap G_{\delta}}.

Ist {D} eine {F_{\sigma}} Menge so ist es abzählbare Vereinigung abgeschlossener Mengen, und diese abgeschlossenen Mengen sind nach vorherigem {G_{\delta}}-Mengen, also ist {D} abzählbare Vereinigung von {G_{\delta}}-Mengen und damit {D \in G_{\delta\sigma}}. Analog folgt {G_{\delta} \subseteq F_{\sigma\delta}}. {\square}

Nochmal übersichtlich, Pfeile zwischen den Mengen von links nach rechts bedeuten die linke Menge ist in der rechten enthalten, die senkrechten Linien bedeuten eine Menge liegt in der Menge von Mengen, wenn ihr Komplement in der andereren Menge von Mengen liegt.

uebersicht

Der Beitrag als PDF-Datei.